Ⅰ. 서론

비디오 게임 그래픽 효과 중 여러분의 눈을 가장 즐겁게 해주는 것은 무엇이 있습니까? 동적 그림자, 안개, 하이폴리곤 모델, 등등. 여러 가지 있지만 역시 가장 눈에 띄는 것은 반사 효과라고 생각합니다.

반사 효과는 동적입니다. 사람이나 물체가 이동하면 반사상 안의 물체도 그를 따라 이동합니다. 반사 효과는 화려합니다. 그림자는 검고 볼류메트릭 라이팅은 하얗지만 반사상은 다채로운 색상을 띱니다. 붉게 타오르는 수류탄의 불꽃, 푸른 하늘과 눈부신 태양, 무리지어 날아가는 새떼. 삼라만상이 거울 위에서, 자동차 표면 위에서 춤을 춥니다. 반사상은 또 하나의 세계를 표현합니다.

인간은 무엇을 아름답다고 여길까요? 반짝이는 보석, 밤하늘의 은하수, 최신 아이폰까지…. 우리가 어떤 것을 아름답다고 생각하게 만드는 기준이 무엇일까요?

좋아하는 것, 갖고 싶은 것, 꼭 있어야 하는 것은 아름답다고 인지합니다. 태양은 지구상의 모든 생명에게 그런 면에서 생명이 살아가는 데 가장 필요한 것, 물이 아름다운 것은 인지상정이겠죠?

물을 자세히 봅시다. 아름다운 구석이 어디 있습니까? 강렬하게 반짝이는 햇빛의 조각, 하늘의 색을 닮아 푸르게, 혹은 붉게 빛나는 수면. 자세히 들여다보면 자신의 얼굴이 보이기도 합니다. 물을 아름답게 만드는 이 다양한 요소들은 모두 반사와 관련이 있습니다. 시각적 즐거움을 제공하는 데 반사의 지분이 상당합니다.

어디 물 뿐입니까? 금이나 다이아몬드 같은 보석, 형형색색의 스테인드 글래스 등 반사 덕분에 아름다운 물체는 굉장히 많습니다.

그래서 그래픽스 엔지니어들은 반사를 구현하는 데 노력을 아끼지 않았습니다. 2004년에 출시한 하프라이프 2는 실시간 반사가 인상적인 물을 선보였습니다. 2007년작 GTA IV는 자동차 표면에 반사를 넣어 극도의 사실감을 선사했습니다. 최근 엔비디아는 기여코 실시간 레이트레이싱, RTX라는 무시무시한 기술을 들고 와서 반사 기술의 끝판왕을 선보였죠.

이러한 반사들은 어떻게 구현이 될까요? 레이트레이싱은 광선의 경로를 추적한다는 매우 직관적인 방식을 사용합니다만. 다들 아시다시피 그렇게 하면 초당 프레임(FPS)가 1도 안 나오죠. 게다가 2004년에 출시한 하프라이프 2의 물 반사는 레이트레이싱 뺨을 후려갈길 정도인데요? 그 비결이 무엇인지 궁금하지 않으신가요?

우리 함께 게임 엔진에서 사용된 반사 효과에 대해 파헤쳐 봅시다. 프로그래머들이 어떤 똑똑한 눈속임을 사용했는지 말이죠. 생각해 보면 그렇죠? 레이트레이싱 반사 외에는 거진 눈속임일 게 분명합니다. 부족한 컴퓨팅 성능으로도 아름다운 반사를 구현하기 위해서는 금단의 마법, 흑마법이 필요한 법이니까요.

Ⅱ. 평면 반사 Planar reflection

1. 구현

half-life_planar_reflection_animated
Half-Life 2: Lost Coast에서 개발자 코멘터리를 실행한 장면

평면 반사는 하프라이프 2에 등장하는 물 반사에 사용된 기술입니다. 기본적인 원리는 다음과 같습니다. 장면을 일반적인 방식으로 렌더링 하기 전에, 물 위에 반사될 물체들을 한 번, 물 아래 잠겨 있는 물체들을 한 번 따로 렌더링을 합니다. 그리고 두 개의 이미지를 결합해서 반사와 굴절이 이루어진 화면을 만들어 냅니다.

지금부터 단계별로 자세히 알아봅시다. 아래 사진은 제가 OpenGL로 만든 게임 엔진을 이용해 만든 자료 화면입니다.

평면 반사라는 이름답게 물은 평면의 형태로 그려집니다. 화면에 파란색 평면은 삼각형 두 개를 붙여 만든 단순한 사각형입니다. 그리고 화면 좌측 상단을 보시면 두 개의 그림이 보이죠? 위에서부터 각각 굴절상과 반사상입니다. 굴절상에는 물 아래에 있는 물체만 그려지며, 반사상에는 물 위의 물체만 그려집니다.

$planar_reflection_2_refraction$

위 그림은 굴절상 이미지를 그대로 파란색 평면에 씌었을 때의 모습입니다. 걍 파란 평면은 없앤 것이 아니냐고요? 아닙니다. 매의 눈으로 보시면, 원래 파란색이었던 영역은 그렇지 않았던 영역에 비해 좀 더 흐립니다. 최적화를 위해 굴절상과 반사상의 해상도를 조금 낮췄기 때문이죠. 디바의 다리를 보면 흰색 선이 있는데, 이곳이 수면 경계선입니다. 제 말을 믿으세요!

planar_reflection_3_reflection

이것은 반사상을 파란 평면 위에 씌운 모습입니다. 완벽한 거울처럼 생겼죠? 거울을 구현할 거라면 여기에서 밝기만 조금 낮춰주면 완성입니다. 하지만 일단은 물을 만드는 것이 목적이지요! 지금까지 보여준 세 가지 요소, 파란색 평면, 반사상, 굴절상을 이용하여 아름다운 물을 만들어내 보겠습니다.

planar_reflection_4_half_blending

위 그림은 반사상과 굴절상 그림을 50대 50 비율로 섞은 모습입니다. 벌써 어느 정도 물 같이 보이지요? 파동이 1도 없는 엄청나게 잔잔한 물 말입니다.

planar_reflection_5_dudv

일렁이는 효과를 넣었습니다. 이런 걸 구현할 때는 DUDV map이라는 걸 사용합니다. 디바 뒤편의 초록 상자의 반사상을 보시면 일렁이는 모습이 명확하게 보입니다. 먼 지점의 수면은 하늘색이 더 강하게 표현되는데 이는 프레넬 효과가 구현되었기 때문입니다.

이 정도 되면 물 반사 구현은 완성된 셈입니다. 기술적으로는 말이죠. 좀 더 예쁜 물을 만들기 위해서는 일렁임을 조절하거나 색깔을 바꾸는 등 사소한 조정이 필요할 것입니다.

planar_reflection_7_lighting

물 위에 조명 효과를 넣어 주면 좀 더 있어 보이게 됩니다. 여전히 별로 예쁘지는 않은데요. 저는 아티스트가 아니라 엔지니어이므로 여기까지만 하겠습니다. (o_O)a

planar_reflection_8_final

DUDV map, 프레넬 효과 등 여러모로 신경써야 할 부분이 많습니다만. 반사 효과 그 자체에만 집중한다면 그 원리는 상당히 간단합니다. 그렇지 않나요? 반사상과 굴절상을 적절히 생성한 뒤 화면에 물 영역에 오려 붙이면 완성이니까요. 그렇다면 반사상과 굴절상을 만드는 방법도 알아야겠지요?

planar_reflection_9_improved
나중에 좀 예쁘게 만들어 봤는데 어떤가요?

2. 반사상과 굴절상 만들기

사실 굴절상은 별 거 없습니다. 그냥 플레이어 화면 렌더링 할 때랑 똑같은데, 다만 수면 위의 물체들을 잘라내기만 하면 되지요. 이것은 OpenGL의 clipping 평면 기능을 사용해도 됩니다만. 수면 위아래 물체들을 잘라내는 방식에 대해 좀 더 자세히 알아 볼까요?

고등학교에서 기하와 벡터를 배운 분들이라면 평면이 네 개의 스칼라수로 이루어져 있다는 걸 아실 겁니다.

ma-thax + by + cz + d = 0ma-th

그리고 어떤 벡터

ma-thV = (\alpha, \beta, \gamma)ma-th

가 있다고 할 때

ma-th(a, b, c, d) \cdot (\alpha, \beta, \gamma, 1) > 0ma-th

을 만족하면 벡터 $V$는 평면보다 위쪽에 있습니다. 4차원 벡터의 내적 연산이죠. 왜 이렇게 되는지는… 저도 걍 외웠습니다.

아무튼 수면을 기준으로 물체를 잘라내는 방식은 대강 알게 됐습니다. 다음은 카메라를 올바른 위치로 이동시키는 방법인데요. 아까 말씀드렸듯이 굴절상을 만들 때는 카메라 위치가 플레이어 시야의 위치와 똑같다고 했지요. 그러니 반사상 카메라의 위치만 알아내면 되는데요.

일단 제가 OpenGL로 물을 구현할 때에는 굉장히 단순한 방법을 썼습니다. 물은 무조건 수평이니까, 카메라를 그냥 물까지의 거리의 두배만큼 수직 아래로 내리면 되는 거 아니겠습니까?

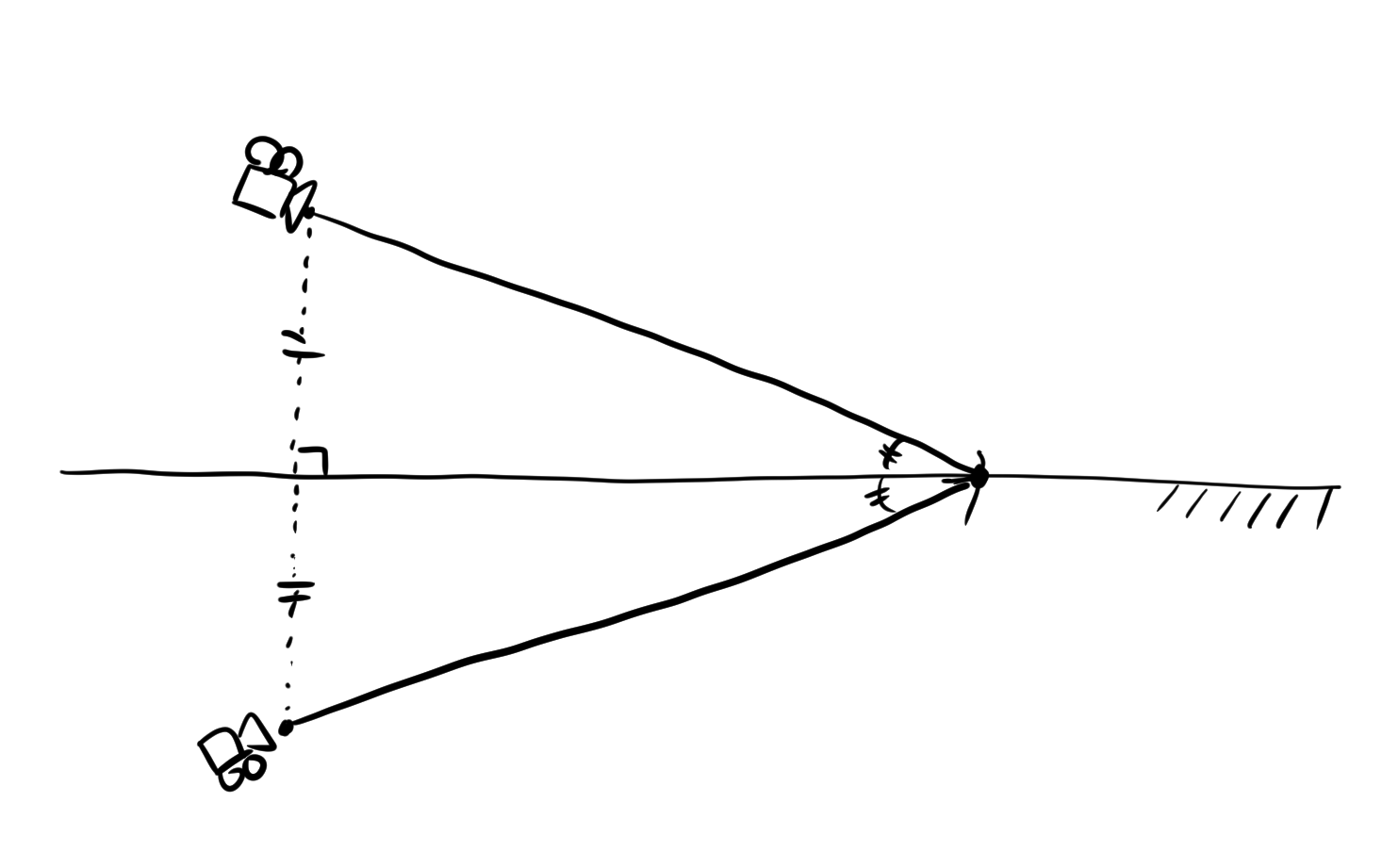
planar_reflection

대충 그림으로 나타내면 이런 모습입니다. 위 카메라는 플레이어 시야이자 굴절상의 카메라이고, 아래 카메라는 반사상의 카메라입니다. 각 카메라는 수면과의 거리과 같으면서 위치는 정반대입니다. 바라보는 방향도 수면을 기준으로 대칭이고요. 반사상의 카메라는 위아래가 뒤집혀 있습니다.

이렇게 완전 수평인 물의 경우는 반사상 카메라를 만드는 게 쉽습니다. 하지만 GTA V 같은 곳에는 거울이 있는데, 거울은 공간 안에 어떤 방향으로도 배치될 수 있지요. 이 부분은 행렬 수학에 대해 깊에 들어가야만 해서 여기서는 생략하겠습니다. 아무튼 행렬 수학을 이용하면 평면이 어떻게 배치되어 있어도 반사상 카메라를 만들 수 있으며, 반사상과 굴절상만 만들어내면 평면 반사를 구현하는 것은 간단합니다!

3. 특징

평면 반사에는 한계가 있습니다. 이름을 보면 알 수 있듯, 평면에밖에 사용하지 못 합니다. 평평한 거울이나 타일 바닥에서만 올바른 반사를 표현할 수 있습니다. 하프라이프 2의 물은 실제론 평면인데 약간의 일렁임 효과만 줘서 물처럼 보이게 했을 뿐이죠. GTA V의 바다처럼 크게 출렁이는 물에는 평면 반사를 사용할 수 없습니다.

그리고 더 큰 문제가 있는데요. 평면 반사는 기본적으로 장면을 세 번 렌더링 하게 됩니다. 물 아래의 물체들을 렌더링 하느라 한 번, 물 위의 물체들을 렌더링 하느라 한 번, 화면에 그릴 장면을 렌더링 하느라 한 번. 물론 수면은 세상을 이등분 하기 때문에 물 위의 물체들 반틈, 물 아래 물체들 반틈만 렌더링 하면 되긴 합니다만. 이 경우에도 물체의 위치를 판별하는 연산이 수행되는 등 값싸지만은 않지요.

하프라이프 2는 옛날 게임이라서 폴리곤 수가 적어 요즘 컴퓨터로는 이 3배 렌더링이 그리 부담이 아닙니다만. 현대의 게임엔 한 화면에 담긴 폴리곤의 수가 비교가 안 됩니다. 수면 반사에 소요될 연산력(computing power)을 아끼면 화면에 다채로움을 두 배 넘게 늘릴 수 있게 됩니다. 그래서 현대의 게임에서는 잘 사용되지 않습니다.

GTA V는 수면 반사와 옷가게의 거울 반사 등 필수적인 상황에는 평면 반사를 사용하긴 합니다. 그러나 좀 더 진보한 반사 구현 방식이 개발되며 평면 반사는 사용되지 않는 추세입니다. 사이버펑크 2077이나 미러스 엣지 카탈리스트에서는 환경맵과 화면공간 반사를 결합하여 거울과 수면의 반사를 구현했습니다. 지금부터 이러한 반사 구현 기법에 대해 알아볼까요?

Ⅲ. 환경맵 Environment map

혹시 360도 사진에 대해서 아시나요? 구글 지도의 스트리트 뷰나 네이버 지도의 로드뷰 기능을 사용해 보신 분들은 다들 아실 텐데요. 시점을 이리저리 움직이며 앞뒤, 위아래, 좌우 모든 방향을 다 둘러볼 수 있는 기능이죠.

이러한 기능을 구현하기 위한 방식은 다양합니다.

상하좌우앞뒤 6개의 방향의 모습을 담은 6개의 그림을 정육면체처럼 붙여서 360도 사진을 완성하면 cube map
출처
마치 공 모양의 지구를 평평하게 펼쳐 지도를 만들 듯 360도 공간을 2차원 이미지로 만든 equirectangular map
출처

이런 다양한 방식을 통해 모든 방향의 모습을 평면 그림으로 담은 것을 컴퓨터그래픽스에서 환경맵(environment map)이라고 부릅니다. 환경맵은 스트리트뷰처럼 색깔 그대로 렌더링 하여 사용할 수도 있으며, 이를 응용하면 스카이박스를 구현할 수 있습니다. 환경맵을 그대로 사용하지 않고 약간의 수학적 연산을 가미하면 물체 표면의 반사상을 찾는 데 사용할 수도 있습니다.

환경맵을 표현하는 방식은 큐브맵, equrectangular map 등 다양한 방식이 있긴 하지만, 각각은 쉽게 상호 변환이 가능합니다. 그래서 저는 큐브맵 형태로 변환해서 사용하는 것을 선호하는 편입니다. 따라서 이후로는 큐브맵에 대해서만 설명토록 하겠습니다.

1. 큐브맵 사용 방법

출처

큐브맵은 상하좌우앞뒤 총 6개의 이미지로 이루어져 있습니다. 이것을 마치 주사위 만들 듯 접어 붙이면 모든 방향을 커버하는 하나의 큐브가 되지요. OpenGL에서도 큐브맵을 만들 때 -X, +X, -Y, +Y, -Z, +Z 여섯 개의 텍스처 각각에 해당 방향에 맞는 이미지를 넣어서 생성합니다.

그리고 이를 렌더링 과정에서 사용할 때는 3차원 벡터를 이용합니다. 보통 2D 이미지는 가로축, 세로축 두 개의 숫자로 이루어진 좌표로 픽셀을 선택하죠? 큐브맵은 $(2.1, 3.8, 2.5)$처럼 3차원 벡터를 이용, 해당 방향에 있는 픽셀의 색깔을 얻습니다. 이때, 텍스처에서 색깔을 얻어오는 작업을 샘플링 sampling이라고 합니다.

출처

큐브맵 샘플링에서 유의미한 건 벡터의 방향 뿐, 벡터의 길이는 아무런 상관이 없습니다. 그래서 벡터 $(1, 0, 0)$과 $(12, 0, 0)$은 완전히 같은 지점을 샘플링 합니다.

큐브맵 이미지를 생성하는 것은 굉장히 품이 많이 드는 작업입니다. 6개의 방향이 있으므로 장면을 총 6번 렌더링 해야 합니다. 평면 반사는 반사상, 굴절상 두 개만 만들면 되는 것에 비하면 훨씬 비싸지요.

대신 평면 반사를 위해 만든 반사상과 굴절상은 카메라를 조금이라도 움직이면 못 쓰게 됩니다. 상의 위치가 어긋나서 반사상을 알 수 없는 지점이 생기니까요. 그러나 큐브맵은 단 한 번 만들어 두면 100번이고 1,000번이고 재사용 할 수 있습니다. 상이 좀 어긋나긴 해도 반사상이 누락되는 현상은 없으니까요.

하프라이프 2 등 소스엔진 게임에서는 모든 큐브맵 이미지를 사전에 생성해 두는 방식을 취합니다. 한편 GTA V에서는 자동차 표면 반사를 위해 큐브맵을 만드는데요. (참조) 매 프레임 새로 생성하는 대신 해상도를 아주 작게 해서 성능 하락을 줄이는 전략을 택했습니다. 최신 게임들은 모두 GTA V 같은 방식을 사용합니다.

2. 큐브맵 반사 Cube map reflection

먼저 다음 영상을 봐주세요.

보시면 플레이어가 움직이면 반사상도 함께 따라오는 모습을 볼 수 있을 것입니다. 큐브맵 반사의 큰 특징이죠. 그리고 영상 후반부에는 Parallax Corrected라는 것이 나오는데, 언뜻 보기에 완벽한 반사처럼 보입니다. 이것도 아래에서 설명하도록 하겠습니다. 우선은 전반부에서 보여준 사람을 따라다니는 반사에 대해 이야기해 보겠습니다.

큐브맵 반사는 하프라이프 2에서도 사용됐을 정도로 오래된 기술입니다. 동시에 최신 게임에서도 매우 유용하게 사용됩니다. 게임에서 사용되는 큐브맵 반사의 예는 다음과 같습니다.

하프라이프 2에서 물 외에 거의 모든 반사
GTA V의 차동차 표면 반사
둠 이터널

환경맵 반사는 거의 모든 게임에서 사용됩니다. 게다가 그 유명한 물리 기반 렌더링(Physically based rendering, PBR)에서 반사를 구현하는 데 큐브맵은 필수적입니다. (언젠가 이것에 대한 글도 쓰도록 하겠습니다!)

게임을 하면서, 눈썰미가 좋으신 분들이라면, 큐브맵 반사는 굉장히 이상하게 작동한다는 것을 눈치채셨을 겁니다. 특히 하프라이프 2나 카운터스트라이크를 많이 하신 분이라면, 자신이 움직이면 반사상이 자신을 따라다니는 것처럼 느껴지는 현상을 겪어 보셨을 겁니다. 왜 그런 현상이 일어나는지는 큐브맵 반사를 구현하는 원리를 이해하면 알 수 있습니다.

수학적 얘기

여기서부터는 수학적인 이야기를 좀 할 텐데요. 어렵다면 굳이 완전히 이해할 필요는 없습니다. 여기서 중점사항은, 반사를 구현하는 방법이 다 수학이구나 하는 것만 알고 넘어가 주시면 되겠습니다.

장면을 렌더링 할 때 어떤 점 $P$의 색깔을 결정해야 합니다. 그 색깔은 여러분의 모니터 어느 한 픽셀의 색깔이 될 예정인데요. 이때 $P$의 색깔을 정하기 위해 텍스처의 한 픽셀의 색깔을 사용할 것이고 거기에 조명으로 인한 효과도 적용하겠죠? 그리고 반사상을 그리기 위해서는 반사될 물체의 색깔도 알아내야 합니다. 해야 할 일이 상당히 많아요. 그렇지만 이 글의 주제는 반사이므로 반사상의 색깔을 알아내는 문제에 대해서만 생각해 봅시다.

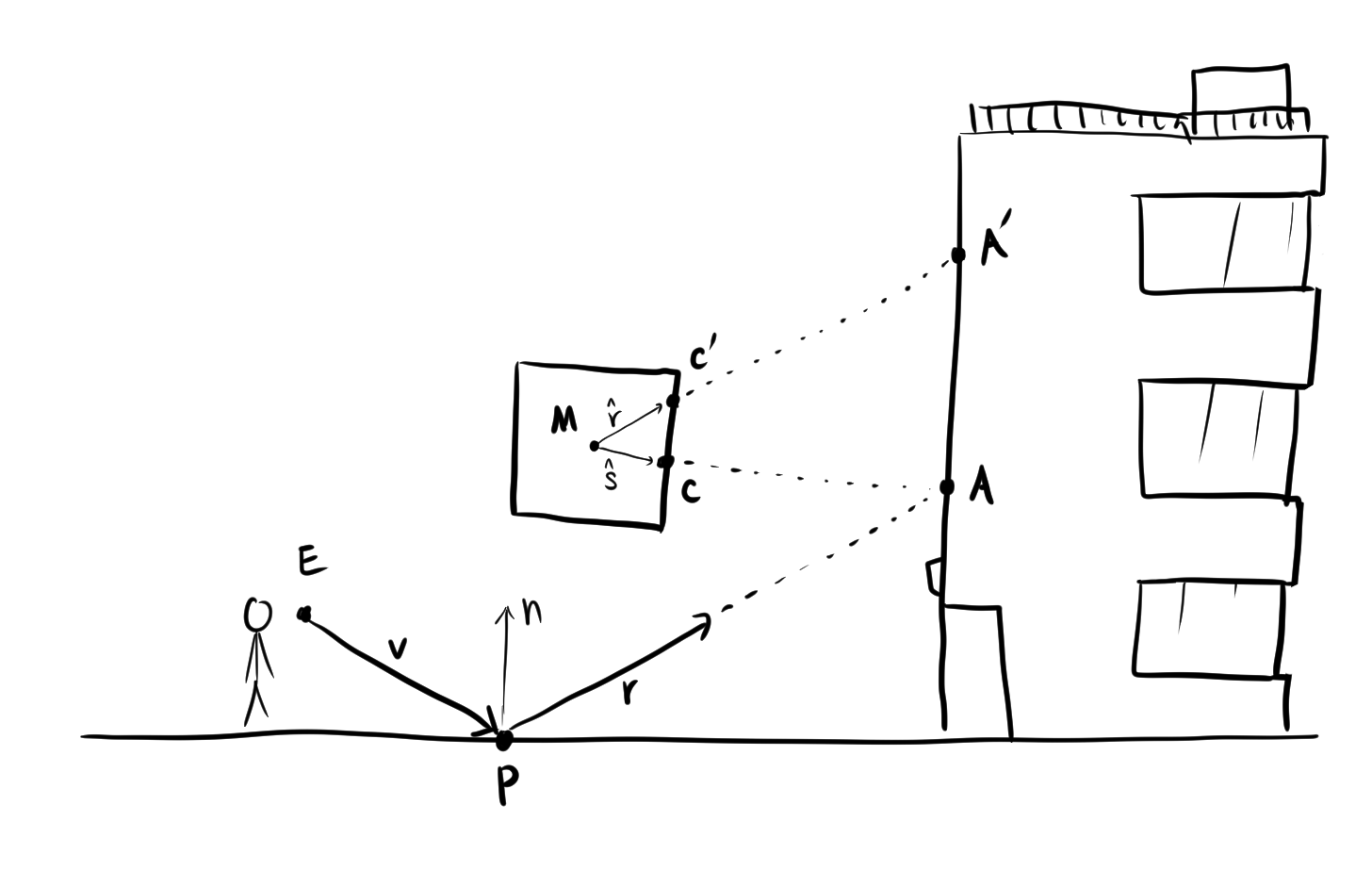
cubemap_graphic

우선은 점 $P$ 위에서 반사될 물체의 위치를 찾아내야 하는데요. 여러분의 눈 위치를 점 $E$라고 뒀을 때, $v = P - E$로 view 벡터 $v$를 구합니다. 여기서 $v$, $P$, $E$ 모두 3차원 벡터입니다. 그리고 물체의 표면으로부터 수직 방향을 가리키는 normal 벡터 $n$이 있습니다. 이제 다음과 같은 공식을 이용해 반사 벡터 $r$을 얻을 수 있습니다.

ma-thr = v - 2(v \cdot \hat{n})\hat{n}ma-th

이때, 어떤 벡터 $x$ 위에 모자를 씌우면($\hat{x}$) $x$와 가리키는 방향은 같으면서 길이는 1인 단위벡터를 뜻합니다.

ma-th\hat{x} = \frac{x}{||x||}ma-th

그림에 있는 화살표 $r$이 바로 반사 벡터입니다. 이제 반사 벡터가 가리키는 방향을 따라가서 건물과 닿으면 그 지점이 바로 반사상의 위치 $A$가 됩니다. $A$ 위치에서 건물의 텍스처 색깔을 가져오면 그것이 바로 반사상의 색깔이 되는 것이죠. 이것으로 문제가 해결되었습니…다?

아닙니다! 방금전 문장에 대해 찬찬히 생각해 봅시다. 반사 벡터가 가리키는 방향을 따라간다. 이 지극히 단순한 문장을 컴퓨터가 실행한다면, 구체적으로 어떤 연산을 가리킬까요? 그렇죠. 레이트레이싱입니다. 벡터 $r$이라는 광선을 발사하여 건물 표면에 닿는 점 $A$를 계산한다, 정확하게 레이트레이싱이죠.

아시다시피 레이트레이싱은 RTX 그래픽 카드를 갖고도 매우 오래 걸리는 연산입니다. 그리고 당연하게도 2004년 게임인 하프라이프 2에서 레이트레이싱을 사용할 수는 없었을 것입니다.

여기서 큐브맵이 등장할 차례입니다! 그림에서는 점 $M$이 바로 큐브맵 위치입니다. 그리고 $M$을 감싸는 사각형은 $M$ 주변 공간의 색깔 정보가 저장된 큐브맵 이미지를 나타냅니다. 큐브맵 반사에서는 $M$에서 출발하는 반사 벡터 $\hat{r}$을 이용해 큐브맵 위 $c’$의 색깔을 샘플링하여 반사상의 색깔을 가져옵니다.

그런데 $\hat{r}$의 연장선을 그어보면 $A’$를 가리키고 있습니다. 사실 정확한 반사상의 위치는 $A$지요? 그래서 정확한 반사상 색깔을 찾으려면 $\hat{s}$을 사용해 큐브맵 이미지의 점 $c$를 샘플링해야 되는데요. 레이트레이싱 없이는 $A$를 찾을 수 없으므로 $\hat{s}$도 찾을 수 없습니다. 그래서 어쩔 수 없이 $A’$의 반사상을 사용하는 것으로 타협을 보게 되는 부분입니다.

여기서 여러분이 앞으로 걸어가는 상황을 생각해 봅시다. 그러면 여러분의 새로운 위치 $E_1$에서 아까랑 같은 각도에 위치한 새로운 지점 $P_1$가 있겠죠. 그러면 새로운 view 벡터 $\hat{v}_1$은 이전의 $\hat{v}$ 와 정확하게 동일하며 따라서 반사상의 색깔도 그대로입니다. 이것이 의미하는 바는, 여러분이 아무리 앞뒤로 움직여도, 여러분 입장에서 $v$ 방향에는 언제나 같은 반사상이 위치하게 된다는 것입니다. 이것은 위에 있는 소스엔진 큐브맵 반사 영상에서 확인해 보실 수 있습니다.

바닥이나 거울처럼 넓은 면적에서 일어나는 반사를 구현할 때는 큐브맵이 참 별로입니다. 그런데 큐브맵 반사의 특징은, 점 $P$와 큐브맵 위치 $C$의 거리가 가까울수록 $A$와 $A’$의 차이가 적어진다는 점입니다.

그래서 상대적으로 크기가 작은 물체 안에서 큐브맵 이미지를 생성하면 사람 눈으로는 왜곡을 전혀 눈치챌 수 없는 거의 완벽한 반사를 구현할 수 있게 됩니다.

수학 내용을 건너뛰었습니까?

그렇다면 핵심만 짚고 넘어가도록 하겠습니다.

반사상의 색깔을 알아내는 작업은, 해당 지점에서 어떤 방향에 어떤 물체가 있나 알아내는 작업임
레이트레이싱을 이용하면 그 방향으로 광선을 쏘아서 알아낼 수 있지만 너무 고사양이 요구됨
그래서 그냥 큐브맵의 해당 방향 색깔을 이용하는 것으로 타협을 봄
큐브맵의 약점 때문이 반사상이 정확하지 않음

3. 시차교정 큐브맵 반사 Parallax corrected cube map reflection

한 가지 생각해 봅시다. 반사상의 위치 $A$를 찾을 수 없는 이유가 무엇입니까? 레이트레이싱이 너무 비싼 연산이라 그렇습니다. 그럼 레이트레이싱 없이 반사상의 위치 $A$를 찾을 수 있다면 문제가 해결되는 거 아닐까요?

아이디어가 하나 있습니다. 주변 공간의 모양을 단순한 도형으로 근사(approximate)하는 것입니다. 가령 직육면체 모양의 방을 생각해 봅시다. 이 안에는 창문이나 액자, 화분 같은 다양한 물체가 들어 있습니다. 하지만 이런 세세한 디테일을 무시하고 오직 직육면체만을 대상으로 하여 레이트레이싱을 수행하는 것입니다.

이 방법을 사용하면 아주 정확한 $A$를 찾을 수는 없지만 $A$에 훨씬 가까운 $A’$를 찾아낼 수 있게 됩니다. 이것이 바로 시차교정 큐브맵 반사의 기본적인 아이디어입니다.

cubemap_graphic

다시 아까 그 그림을 가져와 보겠습니다. 레이트레이싱으로 점 $A$를 찾으려면 저 건물의 수많은 삼각형과 교점 검사를 해봐야 할 것입니다. 건물 모양을 딱 보니 삼각형 개수가 적어도 수십 개 수준은 되겠군요. 그러는 대신, 건물을 하나의 거대한 직육면체라고 생각한 뒤, 직육면체에만 광선을 쏴본다면 훨씬 빠를 것입니다. 직육면체는 12개의 삼각형, 혹은 6개의 평면으로 표현될 수 있어 훨씬 경제적입니다.

이것은 제가 OpenGL로 구현한 시차교정 큐브맵 반사입니다. 저는 직육면체 방을 6개의 평면을 이용, 각각에 광선을 발사하여 가장 가까운 점을 $A$로 선택하는 방식으로 구현했습니다. 그래서 방의 형태는 볼록 다면체여야만 합니다. 대신 볼록하기만 하다면 육면체, 십이면체 아무리 복잡해도 상관없습니다. (볼록한 도형의 특징은 다분히 수학적인 내용이므로 여기를 참조해 주세욧.) 아울러 영상 후반부에는 다른 건 다 빼고 큐브맵 이미지만 보여주는 부분이 있는데요. 꽤나 흥미로울 거라 생각합니다.

사실은 복잡한 공간을 단순화하는 기법이기 때문에 그 한계점은 명확합니다. 우선은 제가 그림으로 표현한 것은 탁 트인 공간에서 건물에만 광선을 발사하는 상황을 가정했는데요. 광선이 아무 곳에도 도달하지 않는 경우는 어떻게 해야 할까요? 충돌을 하면 시차교정 매핑을 하고 충돌하지 않으면 일반 큐브맵 매핑을 한다? 이렇게 하면 시각적으로 별로 예쁘지 않습니다. 그래서 일반적으로 시차교정 큐브매핑은 상하좌우가 모두 폐쇄된 실내에서만 사용할 수 있습니다.

한편, 실내의 구조가 복잡할수록 이 기법의 한계가 더 크게 드러납니다. 위의 소스엔진 영상에서는 직육면체의 방만 나왔었죠? 만약 방 한가운데 기둥이 있다면 어떻게 될까요? 직육면체 방은 볼록 다면체이므로 평면 6개만 사용하여 표현될 수 있습니다. 그런데 기둥이 생기면 더이상 방의 형태는 볼록하지 않게 되므로 삼각형으로 표현할 수밖에 없게 되며, 이는 컴퓨팅 파워를 엄청 잡아먹습니다.

그 외에도 큐브맵은 본질적으로 만드는 데 시간이 많이 걸리기 때문에 실시간으로 움직이는 물체는 반사되지 않는다는 문제점이 있죠.

이러한 문제점을 보완하기 위해 다음에 설명할 화면공간 반사와 결합하여 사용됩니다.

Ⅳ. 화면공간 반사 Screen space reflection를 더하자

기본적인 내용은 제가 이전에 작성한 글 RTX란 무엇인가 2편 - 레이트레이싱 이전의 기술을 읽어 주세요!

위 내용을 잘 읽어보셨다면 화면공간 반사의 장점과 단점을 이해하셨을 겁니다. (어려웠다면 댓글로 말씀해 주세요.) 장점은 실시간으로 변하는 장면을 반사에 반영할 수 있으면서도 컴퓨팅 파워도 적게 소모한다는 점이구요. 단점은 화면에 나타나지 않는 물체는 반사되지 못 한다는 점이죠. 그러니 여기서 큐브맵 반사와 화면공간 반사를 함께 사용하여 둘의 장점만 취할 수 있게 됩니다.

기본적인 아이디어는 간단합니다. 화면공간 반사상을 찾기 위해 광선을 쏴보고, 반사상이 화면 바깥에 있으면 큐브맵을 사용하는 것입니다. 이게 전부입니다. 간단한 아이디어지만 게임에서 사용되면 완벽에 가까운 반사를 구현할 수 있습니다.

위 영상은 미러스엣지 카탈리스트에서 찍은 것입니다. 보시면 RTX 부럽지 않은 완벽한 반사를 보여주는데요. 시야를 아래로 내려보면 반사상이 흐려지는 걸 보니 확실히 화면공간 반사는 맞는 모양입니다.

그런데 고개를 숙이고 이리저리 움직여 보면, 흐릿한 반사가 나름 방의 모양과 잘 맞는 모습을 볼 수 있지요? 이것이 바로 시차교정 큐브맵 반사입니다.

사실 여러분은 게임을 하면서 위나 아래를 보고 다니지 않죠? 일반적인 상황에서는 앞을 보고 돌아다닙니다. 그래서 화면공간 반사에 필요한 반사상이 모두 화면에 포착이 되는 경우가 많습니다. 그리고 일반적인 상황이 아닐 때 큐브맵으로 보완, 실내에서는 시차교정까지 구사함으로써 약점을 최대한 보완하는 것이 기본 전략입니다.

혹시 여러분들은 이 글을 읽기 전까지 미러스엣지에서 반사의 이상한 부분을 눈치채지 못 하셨을지 모르겠네요. 이런 태크닉이 사이버펑크 2077, 배틀필드 5, GTA V 등 다양한 게임에서 사용되었다는 사실을 알고 계신가요? 게임 엔진 개발자들은 플레이어들이 반사의 이상한 점을 눈치채지 못 하게 만들려고 많은 노력을 하고 있습니다. 제가 게임 엔진의 환상을 깨버렸다면 죄상한 부분이구연. ㅎㅎ

Ⅴ. 마치며

반사는 아름답습니다. 게임 엔진 개발자들은 초창기 때부터 이를 잘 인지하고 있었으며, 자신의 게임에 구현해내기 위해 많은 노력을 기울여 왔습니다. 일반인인 우리 입장에서 보기에, 이런 아름다운 반사가 사실은 오로지 수학의 힘으로 만들어졌다는 것은 놀라운 점입니다. 뭔가 고딩 때 수학 공부를 열심히 하지 않은 것에 대한 후회가 물밀들이 밀려옵니다.

만약 수학 선생님이 게임 엔진의 원리를 잘 알고 있어서 수업에 이러한 내용을 접목시킬 수 있다면 어떨까 싶습니다. 기하와 벡터 단원만 보면 말이죠. 평면과 선분의 교점 구하기 문제는 발사된 총알이 적을 명중했는가 검사하는 사례를 통해 설명할 수 있겠구요. 벡터의 내적의 성질에 대해서는 Separate Axis 정리라던가, 조명의 위치에 따른 물체 표면의 밝기 같은 문제로 보여줄 수 있겠네요. 적문 문제는 대기 산란 모형(atmospheric scattering models)을 이용, GTA V 스크린샷을 보여주며 가르치면 어떨까 싶습니다.

여러분도 게임에서 사용되는 수학에 대해 알아가면서 수학에 대한 재미를 길러 보시면 어떨까요? 이상, 문과 수학 4등급 받은 수포자 게임 엔진 개발자였습니다. 감사합니다!

요약

이름	장점	단점
평면 반사	가장 정확한 반사 물체의 변화 실시간 반영	렌더링 속도가 너무 느려 사양되는 추세
큐브맵 반사	한 번 큐브맵 생성하면 이후엔 낮은 비용으로 반사 구현 흐린 반사상 구현 가능 (거친 표면 등)	반사상 위치가 어긋남 (시차교정으로 제한적 개선 가능) 실시간 변화 반영이 어려움
화면공간 반사	정확한 반사상 흐린 반사상 구현 가능 낮은 비용으로 실시간 변화 반영 가능	반사상 누락 가능성

게임이 반사를 구현하는 방법